Previously, we looked at five trends related to algebra on the SAT Math test and how to approach a question centered around each test. But of course, there is much more on the SAT Math section than just algebra! This time, we’ll turn our attention to the types of geometry problems that have been appearing more often and the tricks that you can use to ace each one of them!
Special Right Triangles
The first SAT Geometry trend we will discuss is less about memorizing a trick and more about knowing what resources are available during the test. Below, we can see the Reference Sheet provided on the front of every SAT Math section.
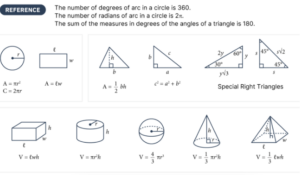
While plenty of useful formulas and reminders are on this page, one of the most useful (and least utilized) is the Special Right Triangles. This reference provides us with the side length ratios for triangles that have angles measuring 30°/60°/90°, or 45°/45°/90°. Not only do these triangles tend to show up more than you expect, but they often appear in unexpected places, so it’s essential to be aware of them.
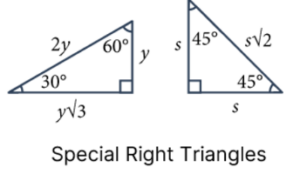
Let’s look at a sample SAT problem that can be solved using Special Right Triangles:
|
Problem:
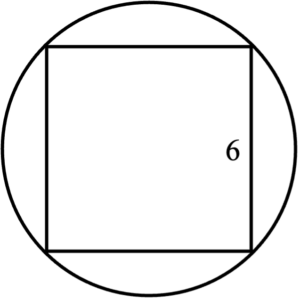
A square with side length 6 is inscribed in a circle, as shown above. What is the length of the radius of the circle?
|
It may be surprising that this problem can be solved using Special Right Triangles because it doesn’t appear that there are even any triangles involved. However, we can create a 45°/45°/90° triangle by drawing in a diagonal ofthe square, as shown on the right. 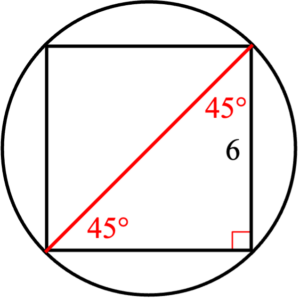
We know that each of the legs of this triangle has a length of 6, so using the reference provided, we know that the hypotenuse of this triangle will have a length of 6√2.
Unfortunately, the hypotenuse that we created is a diameter of the circle, rather than a radius. So our final step will be to divide our diameter by 2, giving us a radius with length 3√2.
Know the Basic Transformations
If you intend to take the SAT soon, one of the first things you should do is to memorize the basic transformations that can be applied to functions. Though more transformations could be applied to functions, the SAT tends to focus on these four
Function Transformation Rules:
- f (x) → f (x+a): shift graph left a units
- f (x) → f (x-a): shift graph right a units
- f (x) → f (x)+a: shift graph up a units
- f (x) → f (x)-a: shift graph down a units
Let’s look at a sample SAT problem that can be solved using these Function Transformation Rules:
|
Problem:
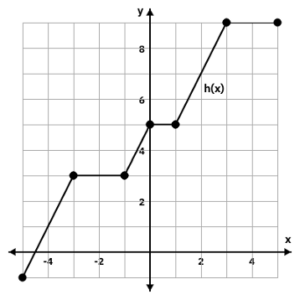
The graph of the function h is shown in the xy-plane above. What is the y-intercept of the graph of y = h(x – 3)?
|
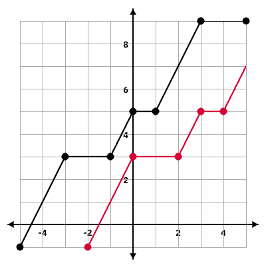
Since this problem is asking us about the function h(x – 3), we know that we will have to shift the given graph 3 units to the right. The easiest way to do this is to move each point on the graph individually and then connect the dots. Once we have drawn in our new graph (as shown on the right), we can see that it crosses the y-axis at the point (0, 3).
Identify Similar Triangles
Identifying Similar Triangles is one of the most important geometry-related skills on the SAT, simply because they often show up. The good news is that the rule for identifying similar triangles is pretty simple: if two triangles have two of the same angles, they are similar. There are technically a couple of other ways to determine if triangles are similar, but the 2-angle method is the most useful on the SAT.
Let’s look at a sample SAT problem that can be solved using Similar Triangles:
|
Problem:
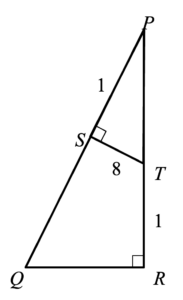
In the diagram above, PQ is perpendicular to ST, and PR is perpendicular to QR. If PS = 15, ST = 8, and TR = 13, what is the length of QS?
|

It may be difficult to tell at first that triangles △PST and △PRQ are similar. However, since ∠P is an angle for both triangles, and both triangles contain a right angle, we know that the triangles must be similar because they have 2 of the same angles.
However, we need to do some additional work before we can use this fact. First, we can use the Pythagorean theorem to get that PT, = 17, which means that PR = 17 + 13 = 30. Then, because we know that our triangles are similar, we can set up a proportion with the side lengths that we know, carefully matching up the sides that correspond with each other (longest with longest, shortest with shortest, etc).

Solving this gives that PQ = 34, and after subtracting 15 to remove PS, we get QS = 19.
Sine and Cosine of Complementary Angles
If you’re not a big fan of trigonometry (sine, cosine, tangent, etc.), you shouldn’t be too worried about the SAT. You should certainly brush up on the basics, but the fact is that the SAT tends to feature little trigonometry, particularly when compared to the ACT.
That said, the SAT likes to ask trigonometry questions that can be solved with a simple (but not-that-widely-known) trick concerning the Sine and Cosine of Complementary Angles. In case you forget, two angles are complementary if the sum of their measures is 90°. This trick tells us that if two angles are complementary, then the sine of one of those angles is equal to the cosine of the other angle. As an example, sin(20°) = cos(70°) and sin(70°) = cos(20°), because 20° + 70° = 90°.
Let’s look at a sample SAT problem that can be solved using the Sine and Cosine of Complementary Angles:
|
Problem:
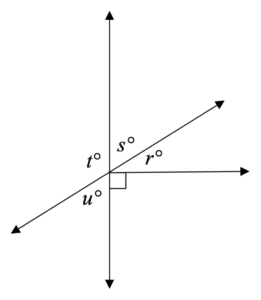
|
Thanks to our trick, we only need to figure out which angle in this diagram is complementary to u. Technically, u could be complementary to itself, but that is not something that must be true, so we will eliminate that answer. Angle s is congruent to u, because they are vertical angles, but they are not complementary. Angle t is supplementary to u (they add up to 180°), but they are not complementary.
That only leaves angle r, which is complementary to u. This may be difficult to see at first, but it is much easier to tell that angles r and s are complementary because they form a right angle, and as we mentioned before, s is equal to u.
Because angles u and s are complementary, we know that sin(u°) = cos(s°).
Use the Radius
One of the clearest trends we have noticed in the SAT recently is the rise in problems involving circles. In particular, we have seen more and more issues that can’t be solved with a simple rule but require some element of creativity and problem-solving.
While there is no strategy that will be able to solve every problem like this, a common theme of these concerns is that it is often helpful to draw in a radius of the circle. Additionally, it is essential to remember that every radius of a circle will be the same length.
Let’s look at a sample SAT problem that can be solved by Using the Radius:
|
Problem:
|
Our first step in solving this issue will be to draw in a radius connecting the center of the circle to the angle formed on the right. In doing this, we have created two triangles inside of our circle. However, we can notice that both triangles have two sides that are each a radius of the circle, meaning that they are all the same length. Therefore, both of these triangles are isosceles.

Knowing that these triangles are isosceles allows us to use the given angles to fill in the missing angles. Finally, we know that the sum of the angles at the center of the circle must add to 360°, so we can simply subtract 110° and 140° from 360° to find that y is equal to 110.

 Which of the following values must be equal to sin(
Which of the following values must be equal to sin(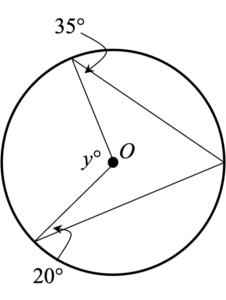 The point
The point 

