Cylinders, circles, and squares; oh my! SAT Geometry doesn’t have to be scary because here at Zinkerz, we closely monitor trends in the SAT to bring our students the most up-to-date test-taking strategies to best utilize their study time. Triangles seem to be the latest trend, and there is quite a bit of variety in the way triangles are incorporated into the SAT. We’ve noticed similar triangles, proofs, special right triangles, hidden triangles, and even trigonometric ratios! Let’s take a look at some popular triangle question types and the best ways to solve them!
Similar Triangles
There is a strong possibility that you will see a question that will require using the fact that two triangles are similar. To use similar triangles to your advantage, you will need to be able to recognize and prove that they are, in fact, similar. Recall the three theorems we can use to prove two triangles are similar:
- Angle-Angle (AA) – If two angles in a triangle are equal to two angles in another triangle, the two triangles are similar.
- Side-Angle-Side (SAS) – If two sides of a triangle are in the same proportion as the two corresponding sides of another triangle, and the angle in between the two sides in both triangles are congruent, then the two triangles are similar.
- Side-Side-Side (SSS) – If all three sides of a triangle are proportionally all three sides of another triangle, the two triangles are similar.
Bonus tip! Whenever an altitude is drawn to the hypotenuse of a right triangle, it forms two similar right triangles.
If one of these situations is true, we can use proportions and congruent corresponding parts to help us solve our problem. Let’s look at an example!
Problem 1:
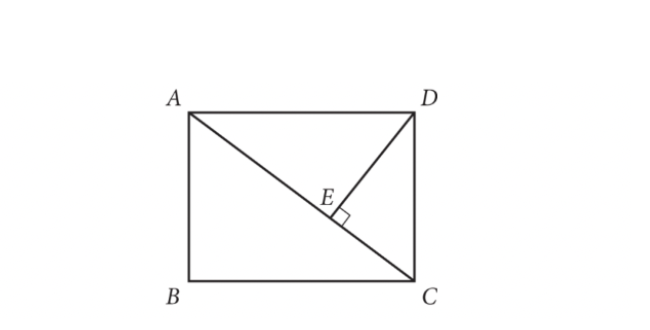
In this case, we know these two triangles are similar because DE is an altitude drawn to the hypotenuse of CAB. Therefore, right triangles CAB and CDE are similar. It can be helpful to draw the two triangles separately to help you create the proportion that will help us solve for the missing length:
The following proportion is made by setting corresponding parts equal to each other. Observe:
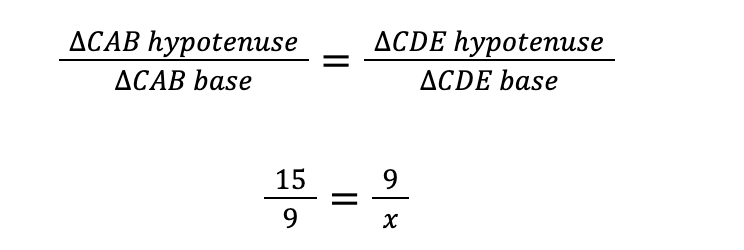
Now, cross-multiply and solve for x:
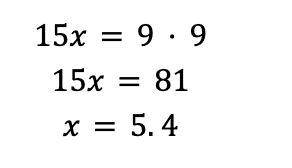
The answer is C.
Proofs
It is also common to see questions involving proofs and triangles. You may be asked to determine the information necessary to prove two triangles are similar (using facts from the example above) or that a triangle is of a certain type (isosceles, right, etc.). Have a look at this question!
Problem 2:
Let’s first recall that an isosceles triangle has a pair of congruent sides and a pair of congruent angles. Since we’re not given a picture of this hypothetical triangle, it may be helpful to draw one to represent the situation.
The first piece of information (I.) tells us that AB is congruent to BC. If this is true, then it is also true that ∠A is congruent to ∠C (angles opposite congruent sides are congruent). This would make triangle ABC an isosceles triangle.
The second piece of information (II.) tells us that ∠A is congruent to ∠C. If this is true, then it is also true that AB is congruent to BC (sides opposite congruent angles are congruent). This would make triangle ABC an isosceles triangle as well.
Since both pieces of information prove that the triangle is isosceles, we should pick answer choice C.
Special Right Triangles
Before you take the SAT, you should familiarize yourself with the reference sheet that will be provided to you. Why memorize formulas when you’ll have them in front of you? Here’s what it looks like:
Not only do we have access to volume and area formulas for triangular shapes, we also see the Pythagorean Theorem and special right triangles rules are given to us as well! Because you won’t need to spend study time memorizing these formulas, you should become comfortable working with this information. You may be asked tough questions because the facts and formulas are readily available. Let’s look at an example that utilizes the special right triangle rules on the reference sheet!
Problem 3:

We should start by drawing a quick sketch of this situation:
Recall that the perimeter is the distance around the outside edge of a two-dimensional shape. Here, we’d like to find the length of each side of the triangle and add them together.
We can see from our sketch that dropping in an altitude (with given height of 53) creates two right triangles within the larger equilateral triangle. Each of these right triangles are actually special right triangles!
Each right triangle is a 30-60-90 triangle. Each angle measure of the equilateral triangle is 60° (since each angle is congruent and they sum to 180°), so one angle in the right triangle is equal to 60°. The 30° measure comes from the altitude splitting the top angle measure in half.
Our special right triangle rules tell us that 5√3=y√3, so therefore, y=5. Finding the length of the hypotenuse will give us one side length of the original equilateral triangle. So, 2y=2(5)=10. Therefore, the perimeter of the equilateral triangle is 10+10+10=10(3)=30.
Bonus tip! Because the question told us the height of the triangle is 53, we should recognize the √3 as an important part of special right triangle rules. The question gave us a little hint!
Hidden Triangles
Sometimes triangles show up in sneaky ways. Questions that appear to exclusively deal with circles oftentimes rely on triangles for a solution. Try to train your brain to “see in triangles” when you’re faced with a tricky question. Let’s try one!
Problem 4:
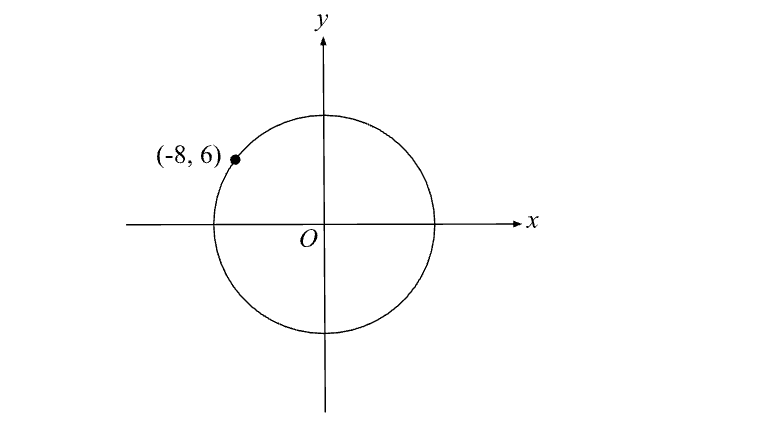
At first glance, this question has nothing to do with triangles. As we look closer, we see that there is a hidden right triangle inside of the circle and that the Pythagorean Theorem may be able to help us!
To find the circumference of a circle, we need the length of the radius. This is where the hidden triangle comes in. Take a look:
The hidden right triangle has a base length 8 and a height of 6, based on the coordinates of the given point. We can now use the Pythagorean Theorem to find the hypotenuse of the triangle, which is also the radius of the circle!
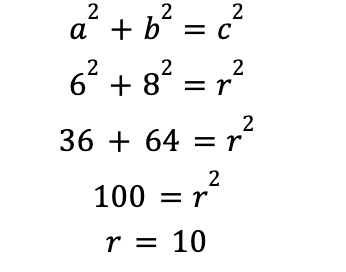
Now that we have r=10, we can find the circumference of the circle and answer the question:
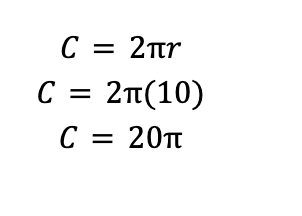
Therefore, the answer is C.
Remember, these formulas are on your reference sheet!
Complementary Angles
While there isn’t usually a lot of trigonometry on the SAT, one particular trigonometric ratio has been showing up recently. Recall these specific complementary angle ratios:
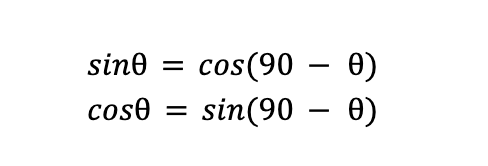
Remember that complementary angles are those who sum is 90°. Let’s look at an example where we need to use these ratios to solve the problem.
Problem 5:
If you can remember the trigonometric ratio for complementary angles, this question is actually quite easy and takes no time at all! Observe that ∠DCA and ∠BCD sum to 90° because they make up the right angle in this right triangle. We know the complementary trigonometric ratios will hold true!
Therefore,
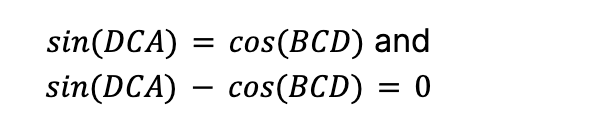
If you see a question involving a right triangle or an angle measure of 90°, and sin and cos, there is a strong possibility that using one of these trigonometric ratios will help you get the answer fast!
The SAT Math section can feel daunting when you’re trying to master every possible topic. Get comfortable with the foundational topics in algebra and geometry and utilize strong study and test-taking strategies. You got this!



